Bạn đang xem: Chứng minh tam giác bằng nhau
A. PHƯƠNG PHÁP GIẢI
1. Ngôi trường hợp bằng nhau trước tiên của tam giác cạnh - cạnh - cạnh (c.c.c)
- Chú ý: mang lại tam giác ABC cùng tam giác A"B"C" thì ta ngầm đọc AB và A"B" là cặp cạnh tương ứng, tương tự như góc A cùng góc A" là cặp góc tương ứng, ...
- Muốn kiếm được cạnh tương xứng và góc tương ứng, ta nên tưởng tượng di chuyển sao mang lại tam giác này trùng khít lên tam giác tê (bởi vì các tam giác có thể ở các vị trí không giống nhau)
- nhì tam giác bằng nhau là hai tam giác có thể chồng khít lên nhau. Khái niệm trùng khít tức là ba đỉnh trùng nhau và tất yếu ba góc tương ứng, bố cạnh khớp ứng cũng trùng nhau.
- Để nắm rõ hơn nếu như trên vở bao gồm hai tam giác ở hai vị trí không giống nhau mà bằng nhau. Ta mang tấm bìa giảm một hình tam giác bởi hình tam giác thứ nhất trên vở, rồi đem tấm bìa đó đặt ông chồng lên hình tam giác thứ hai trên vở vẫn thấy bọn chúng trùng khít lên nhau.
Ví dụ 1: Xem các hình vẽ sau, những đoạn ghi lại giống nhau là rất nhiều đoạn thẳng bằng nhau. Các tam giác nào đều nhau trong hình mẫu vẽ đó.
Hình 1:
Hình 3:
Hướng dẫn:
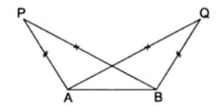
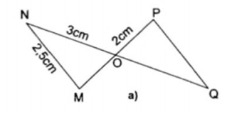
Hình 1: AP = BQ, PB = QA, AB chung.
Vậy $Delta $APB = $Delta $BQA (c.c.c)
Hình 2:
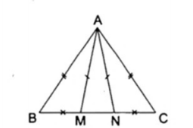
Ta có: AM = AN. AB = AC, BM = CN
Vậy $Delta $ABM = $Delta $ACN (c.c.c)
Ta có: AN = AM, AB = AC với BM = CN.
suy ra BM + MN = NC + MN tốt BN = MC
Do đó $Delta $ABN = $Delta $ACM (c.c.c)
Hình 3:
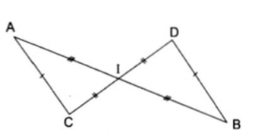
Ta có: IC = ID, IA = IB, AC = DB
Vậy $Delta $IAC = $Delta $IBD (c.c.c)
2. Trường hợp cân nhau thứ nhị của tam giác cạnh - góc - cạnh (c.g.c)
- Theo sản phẩm công nghệ tự cạnh, góc, cạnh tức thị góc đều bằng nhau phải xen giữa hai cặp cạnh khớp ứng bằng nhau.
Lưu ý: Nếu đảo thứ tự: góc - cạnh - cạnh hoặc cạnh - cạnh - góc là ko đúng.
- nhị cạnh cùng góc xen giữa là nhị cạnh này còn có chung điểm đầu cùng điểm đầu đó đó là đỉnh của góc xen giữa cùng hai cạnh của góc đó là hai cặp cạnh tương ứng bằng nhau.
- với tam giác vuông: Ta thấy tất cả các tam giác vuông bao giờ cũng tất cả góc vuông bằng nhau. Đó là góc xen thân hai cạnh góc vuông. Buộc phải trong nhị tam giác vuông nếu có hai cạnh góc vuông tương ứng bằng nhau thì hai tam giác vuông đó bởi nhau.
Kết luận này được gọi là hệ quả.
Hệ trái cũng là 1 trong những định lí cơ mà định lí này được suy ra trực tiếp từ 1 định lí hoặc một đặc điểm toán học
- dấu hiệu góc có thể cho trực tiếp, hoàn toàn có thể gián tiếp chẳng hạn:
Hai tam giác bao gồm một góc chungHai góc đối đỉnhGóc của những đường tuy nhiên song tuyệt vuông gócTia phân giác của góc --> phân chia góc thành nhì phần cân nhau ...Ví dụ 2: mang đến điểm C nằm giữa 2 điểm A cùng B. Trên cùng nửa khía cạnh phẳng bờ gồm chứa đoạn AB vẽ tia Cx cùng Cy làm thế nào cho góc $widehatBCx=60^circ; widehatBCy=120^circ$. Mang điểm E bên trên Ox và điểm F trên Oy sao cho CE = CB, CF = CA. Chứng tỏ AE = BF
Hướng dẫn:
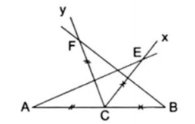
C nằm trong lòng A với B vì vậy $widehatACE+widehatBCE=180^circ$
Mà $widehatBCE=60^circ$ (giả thiết) $Rightarrow widehatACE+60^circ=180^circRightarrow widehatACE=120^circ$
Xét $Delta $ACE cùng $Delta $FCB có:
$widehatACE=widehatBCF=120^circ$
CE = CB, CF = CA
Do đó $Delta $ACE = $Delta $FCB (c.g.c)
Vậy AE = BF (hai cạnh tương ứng)
3. Ngôi trường hợp đều bằng nhau thứ bố của tam giác góc - cạnh - góc (g.c.g)
- trong tam giác bao gồm tổng ba góc trong bằng $180^circ$ đặc thù này có ý nghĩa quan trọng:
Trong các trường hợp đều bằng nhau của tam giác, số nguyên tố góc cho không thực sự hai (vì cho thấy thêm hai góc ta tính được góc thứ ba nên cho thấy ba góc là thừa)
Trường đúng theo hai góc kề với 1 cạnh (trường hợp thứ ba). Trong nhì góc đến nếu bao gồm một góc không kề với cạnh mà bằng nhau thì ta cũng hoàn toàn có thể suy ra góc thứ bố (là góc kề cùng với cạnh bằng nhau) cũng bởi nhau.
- Ứng dụng vào các tam giác vuông $Delta $ABC cùng $Delta $A"B"C" ta có:
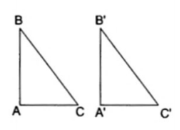
$widehatA=widehatA"
Nếu cạnh huyền BC = B"C"k; chỉ việc $widehatB=widehatB"$ thì suy ra được $widehatC=widehatC"$ (2 góc nhọn phụ nhau). Vậy $Delta $ABC = $Delta $A"B"C" (c.g.c)
Suy ra hai tam giác vuông tất cả cạnh huyền cân nhau và một góc nhọn đều bằng nhau thì nhị tam giác vuông đó bằng nhau.
- Qua bố trường hợp bằng nhau của tam giác thường xuyên ta thấy một tam giác xác định khi biết ba yếu tố. Trong số đó yếu tố góc không thực sự hai.
Ví dụ 3: mang lại $Delta $ABC bao gồm AB = 2cm, AC = 2,5cm, BC = 3cm. Từ A kẻ C"B" // BC, từ B kẻ A"C" // AC, tự C kẻ A"B" // AB. Tính chu vi $Delta $A"B"C"
Hướng dẫn:
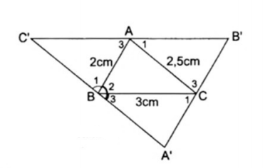
- Xét $Delta $ABC và $Delta $CB"A có:
AC chung
$widehatA_1=widehatC_2$ (B"C" // BC)
$widehatA_2=widehatC_3$ (A"B" // AB)
Do đó $Delta $ABC = $Delta $CB"A (g.c.g)
$Rightarrow $ AB" = BC, CB"=AB (1)
Chứng minh tựa như ta có:
$Delta $ABC = $Delta $A"CB $Rightarrow $ A"C = AB, BA"=AC (2)
$Delta $ABC = $Delta $BC"A $Rightarrow $ AC" = BC, BC"=AC (3)
Từ (1), (2) và (3) ta được:
AB" + CB" + AC" + BC" + A"C + BA" = BC + AB + BC + AC + AB + AC
$Leftrightarrow $ B"C" + B"A" + C"A" = 2.(AB+BC+AC) = 2.(2+2,5+3) = 15cm
Vậy chu vi $Delta $A"B"C" là 15cm.
1. Xem thêm: Xem Phim Giày Thủy Tinh (2002) Tập 39 Vietsub, Giày Thủy Tinh
2. mang đến góc nhọn $widehatxOy$, bên trên Ox với Oy mang điểm A và B làm sao để cho OA = OB. Vẽ hai tuyến phố tròn tâm A và trung khu B có cùng độ dài nửa đường kính (bán kính nhỏ dại hơn OA) chúng cắt nhai tại nhị điểm E cùng F. Chứng minh rằng:
a) $Delta $OEA = $Delta $OEB; $Delta $OFA = $Delta $OFB
b) tía điểm O, E, F trực tiếp hàng
c) FO là tia phân giác của góc $widehatAFB$
3. cho $Delta $ABC. đem điểm B làm chổ chính giữa vẽ mặt đường tròn (B; AC). Rước điểm C có tác dụng trâm vẽ mặt đường tròn (C; AB). Hai tuyến đường tròn này cắt nhau tại hai điểm E và F thuộc nhì nửa mặt phẳng đối nhau bờ là BC
a) chứng minh các tam giác $Delta $ABC = $Delta $ECB = $Delta $FCB
b) chứng tỏ AB // CF, AC // BF
c) chứng tỏ $Delta $ABE = $Delta $ECA
4. mang lại $Delta $ABC bao gồm AB = AC với H là trung điểm của cạnh BC. Chứng tỏ AH vuông góc với BC.
xem lời giải
5. cho góc $widehatxOy$ bên trên Ox rước 2 điểm A và B. Trên Oy mang 2 điểm C cùng D làm sao cho OA = OC; OB = OD. Nối A cùng với D, C với B chúng cắt nhau trên I. Chứng tỏ rằng:
a) $Delta $OCB = $Delta $OAD
b) $Delta $DAB = $Delta $BCD
6. mang lại $Delta $ABC tất cả góc $widehatA=90^circ$. M là trung điểm của cạnh AB. Nối centimet và trên tia đối của tia MC mang MH = MC. Minh chứng rằng HB $perp $ BA
7. mang đến điểm M trên đoạn trực tiếp AB. Trên thuộc nửa mặt phẳng bờ có chứa đoạn thẳng AB, kẻ tia Mx làm thế nào để cho $widehatAMx=60^circ$ và tia My sao để cho góc $widehatBMx=60^circ$. Bên trên tia Mx rước điểm C sao để cho MC = MA; trên tia My rước điểm D làm sao để cho MD = MB
a) triệu chứng mminh AD = CB
b) mang E là trung điểm của AD; F là trung điểm của CB. Minh chứng $widehatEMF=60^circ$
8. đến $Delta $ABC ($widehatA
coi lời giải
10. mang đến $Delta $ABC có $widehatB=widehatC$ (góc A nhọn). Tự B hạ bh $perp $ AC, trường đoản cú C hạ chồng $perp $ AB. Minh chứng rằng $BH = CK
11. cho $Delta $ABC bao gồm đường phân giác của $widehatA$ giảm đường phân giác của $widehatB$ trên O. Trường đoản cú O hạ OE $perp $ AB (E nằm trong AB); OF $perp $ AC (F thuộc AC); OI $perp $ BC (I nằm trong BC). Minh chứng rằng OE = OF = OI
12. cho $widehatxOy$ cùng điểm M nằm trong góc đó. Qua M kẻ mặt đường thẳng song song với Ox giảm Oy trên B và mặt đường thẳng tuy nhiên song cùng với Oy giảm Ox tại A.
a) chứng tỏ MA = OB; MB = OA
b) trên tia đối của tia OA mang điểm C làm thế nào cho AC = AO. Đường trực tiếp CM giảm Oy tại D. Chứng minh rằng centimet = MD.
13. mang đến $Delta $ABC. Từ bỏ A kẻ đường thẳng tuy vậy song cùng với BC. Tự B kẻ đường thẳng tuy nhiên song cùng với AC. Trường đoản cú C kẻ mặt đường thẳng tuy nhiên song với AB. Tía đường thẳng này cắt nhau trên A1, B1, C1. Trường đoản cú A1 kẻ đường thẳng tuy nhiên song với B1C1. Từ bỏ B1 kẻ con đường thẳng song song cùng với A1C1. Từ bỏ C1 kẻ mặt đường thẳng tuy vậy song cùng với A1B1. Tía đường trực tiếp này cắt nhau trên A2, B2, C2. Cứ như thế cho đến khi được $Delta $A10B10C10. đối chiếu chu vi $Delta $ABC và chu vi $Delta $A10B10C10
14. cho góc $widehatxOy$ nhọn. Bên trên tia Ox lấy các điểm M, E, P sao cho OM = ME = EP. Trên tia Oy mang điểm N tùy ý. Tự E và phường kẻ những đường thẳng tuy nhiên song với đoạn trực tiếp MN chúng giảm Oy theo thứ tự trên F cùng Q. Từ N kẻ NI // Ox (I thuộc EF). Tự F kẻ FK // Ox (K ở trong PQ). Chứng minh rằng: ON = NF = FQ















